
JCCC Spline Demo
This is a simple demonstration tool for use in a classroom while teaching lessons on parametric equations, linear interpolations (LERPs) and splines. More functionality and educational content including mathematical basis for LERPs and splines and the ability to combine multiple cubic splines will be added in the future.
A LERP and Spline Primer
Linear Interpolations
LERP is a shortening of the phrase linear interpolation, a mathematical method for finding a value that lies somewhere in between to other values. One can think of a LERP as a weighted average with a parameter, t, representing the balance of the weighting of the two end-point values. Consider two values A and B. These two values can be scalar values such as health points, engine rpms, or mass; they could be vector values such as force, velocity, or position ; or they could be any other quantifiable value such as an RGBA color. The parameter , t, represents the balance of how much A versus how much B we mix to produce our interpolated value, Q. When t is zero, we want Q to be all A with no amount of B. Likewise, when t is one, we want Q to be all B with no amount of A. Mathematically, we can represent this by the following equation
Q = (1-t)*A + t*B.
Smoothly increasing the parameter t from zero to one will smoothly transition Q from A to B. This structure will be the basis of the splines we will construct next.
Quadratic Splines
In order to create a more complex blend, we can add an additional control point, C, that will be our new end point. The blending from A to C will be a combination of two LERPS, one between A and B, and the other between B and C. Also, for clarity of the algebra, we will make the substitution, s = (1-t).
P1 = s*A + t*B, and
P2 = s*B + t*C.
Our final path will be a LERP between P1 and P2
Q = s*P1+ t*P2.
If we substitute the equations for P1 and P2 so that we have Q in terms of our control points, A, B, and C, we get
Q = s*(s*A + t*B) + t*(s*B + t*C),
Q = s2A + stB + stB + t2C,
Q = s2A + 2stB + t2C.
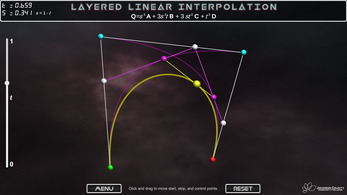
Cubic Splines
We can extend the above work once more by adding a fourth control point, D, and performing at LERP between a quadratic spline of points A, B, and C, and a quadratic spline of points B, C, and D:
P1 = s2A + 2stB + t2C, and
P2 = s2B + 2stC + t2D, so that
Q = s*P1 + t*P2.
Substituting our definitions of P1 and P2 and doing the algebra to reduce terms yields our final equation for a cubic spline.
Q = s*(s2A + 2stB + t2C) + t*(s2B + 2stC + t2D)
Q = s3A + 2s2tB + st2C + s2tB + 2st2C + t3D
Q = s3A + 3s2tB + 3st2C + t3D
You can use these constructs to blend parameters smoothly from one to another. Most commonly, we see this as position, but you can also use these to blend from one rotation to another, one sound clip to another, or even one colour to another. They're easy to code and fast to execute making them fantastic tools for any game programmer.
| Status | Released |
| Category | Tool |
| Platforms | HTML5, Windows |
| Author | J. Douglas Patterson |
| Genre | Educational |
| Made with | Unity |
| Tags | jccc, lerp, mathematics, splines |
| Average session | A few minutes |
| Inputs | Keyboard, Mouse |
| Accessibility | Interactive tutorial, One button |
Download
Development log
- LERP ALL THE THINGS!May 18, 2019





Leave a comment
Log in with itch.io to leave a comment.